the net hack

the background

A while back, Bridget Kromhout (insanely, given our schedules) proposed we give a talk at DevOpsDays Minneapolis on why every technologist should play Nethack.

Curse, bless her now with my fierce tears for reminding me that Nethack existed, and that I’ve spent the past ten-odd years living through save-deaths trying to bring up a Monk. Yes, you can eventually die in 3.4.3 if you keep a game alive too long: I’m meticulous player, who also has more demands on time than playing, so three or four monks were lost in this way.

I managed to get myself too-sick-to-move recently, started playing a bit, and found myself lucky enough to have a game where some bonus-granting rings (Protection, Increate Accuracy, and Increase Damage) were edible. I summoned up the standard neutral Quest Artifacts with the Castle’s wand of wishing, including the Platinum Yendorian Express Card. Like you do.

the menu

For those with lives: in this little game of so dear to some hearts, one can polymorph one’s character into a creature capable of eating some kinds of rings. Eating a ring has a 1 / 3 probability of permanently granting your character the bonus of the ring. The upside is that the character gets the benefit of the ring

• without taking up one of your two ring slots
• without generating hunger from the ring
• without the worry that the ring will be destroyed in some unfortunate way

The downside is the 1 / 1 probability ring is lost during the eating process— leaving your Constant Dungoneer with either the above benefits, or nothing but a slightly fuller belly.

Happy, rings may be “charged,” increasing their bonus. This does come at a cost: there is an enchantment / 7 probability that the ring will be destroyed during the charging process.

Since the PYEC can charge items at no cost to the Constant Dungeoneer, the losses to a character are limited to the the two above probabilities.

the question

So, just how many times should a character charge that +x ring before eating it?

the odds

Having been a poker player in a past life, I long ago worked out the expectation values for charging bonus rings. Having also found myself feeling guilty for wasting time playing Nethack; I thought I’d do something productive, put the game down, and re-sharpen my R skills. A trivial R script is enough to get us some data.

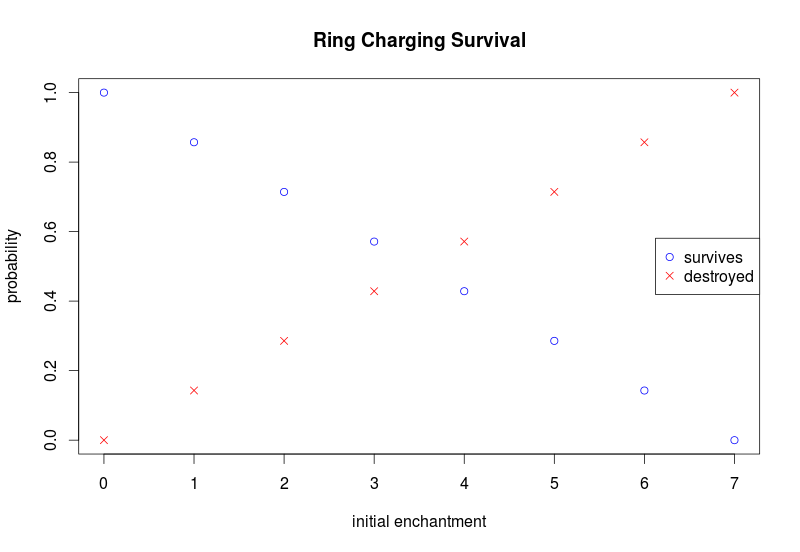
Charging rings with a higher initial enchantment raises the probability that the ring will be destroyed during enchanting. Clearly, we should enchant a +0 ring, because we stand to gain an enchantment with no risk to the ring.

So, when does the probability of getting a higher enchantment outweigh the risks of losing the ring?

The proposition quickly becomes risky as the initial enchantment goes up, while the final enchantment of a surviving ring is increased by a constant (+1). The expectation values can be worked out quite simply.

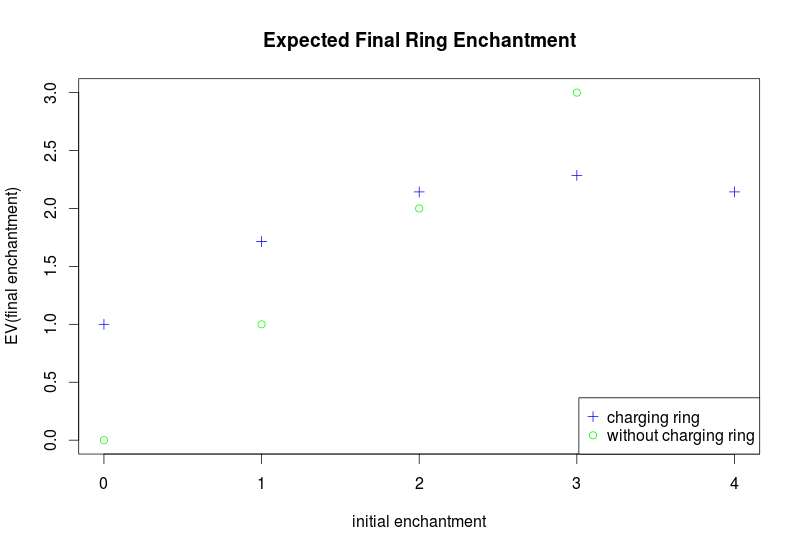
And voila. If we want to maximize the ring enchantment, we should charge a +1 ring: we double the enchantment at a very low 1 / 7 risk of losing the ring in the process. Our potential gains greatly exceed our potential losses.

the philosophy

Now we come to why I decided this was interesting enough to post: the question “Should I charge a ring that currently has a +2 enchantment?”

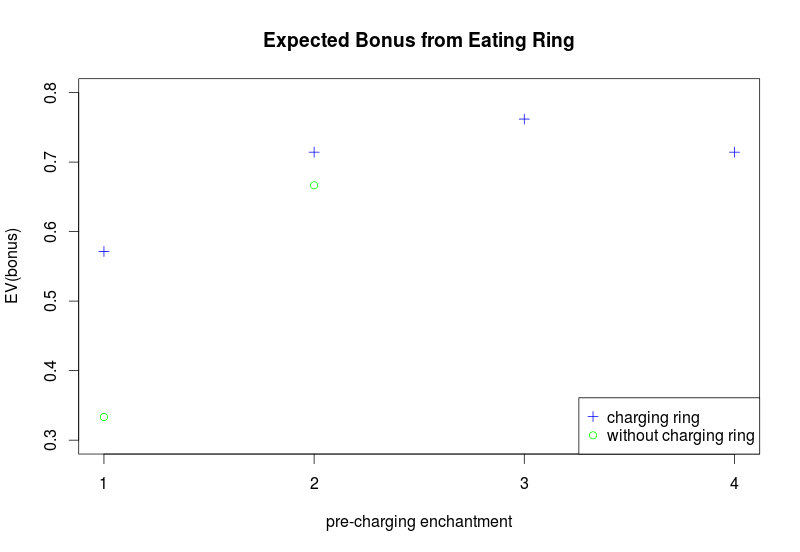
En face, it’s less interesting than I imply. Let’s be clear: we’re gambling with our ring here and probability theory is clear on this matter. What do you do? You take the higher EV— always.

But there are a few ways to interpret probability, and that adds up to more than idle philosophy: the interpretations have real consequences in your theory of gambling.

Why I first say that the proposition is clear is that the Law of Large Numbers and Frequentist probability tell us that, if we perform this experiment on a large number times, the expected value converges with the experiemental (basically Bayesian probability) results to predict the actual bonuses we’ll gain.

If we have the opportunity to play the game of charging or not charging the ring a large number of times, we will gain higher enchantments. Reduced, we should take this gamble once, because it’s a good investment for our risk.

For those of you not addicted to probability theory, I know: Blah, blah.

That’s all fine and good; but if you understand basic probability and the idea of gambling still makes you queasy, you’re probably feeling the effects of something deeploy important and oft misunderstood: risk-of-ruin.

the sure thing

If you want to understand the basic concept behind risk-of-ruin, it’s useful to think of the differences between capital and resources.

As an example: if you’re being offered three-to-one odds on flipping a coin, you should always take the bet if you have the capital. You stand to gain three times your investment half the time, and lose one times your investment half the time. Your expectation value is 1.5. That number is greater than 1. You take the bet. … If you’re playing with capital.

Consider a $1 bet: If you’re blessed enough that $1 doesn’t make a large difference in your survival, you should take the bet. You should play as many times as possible. You lose sometimes, and win sometimes, but gain far more than you lose— as long as losing is a viable option. As long as losing doesn’t risk your life, deplete your stake (so you can’t take this or other positive EV opportunities). Not taking this bet might be due to us falling into the loss aversion trap, but it’s a bad choice to not make the investment.

But consider a case where you need to make rent, which is $1000, and you have exactly $1000. If someone offers you three-to-one odds on flipping a coin for $1000, you shouldn’t take the bet. You’re not playing with a stake. That $1000 isn’t captial to be invested, as wisely as it would be in this case. Here, even playing for $1, you’d get to lose only once before you couldn’t make rent. The costs of losing are too high. All of that $1000 is a needed resource. It’s money, not capital.

the lowdown

If you have one Amulet of Magical Breathing, you might likely keep it and wear it in times of need. If you have two, you’d most likely want to eat one and see if you draw the one-in-three chance that you get to breathe magically without need for the amulet. The first piece of jewlery is most likely a resource, the second is capital.

In the NetHack case a +2 bonus to Protection, Increase Accuracy, and Increase Damage might be nice, but not game-changers.

• If rings are capital to you, charge all the +2 rings you can find, and eat them all.
• If a ring is a required resource, you shouldn’t eat it in the first place: wear it.

This Universe is governed by the laws of probability, but your best choices depend on your situation.